选择排序
思想:选择排序可以说是冒泡排序的改良版,不再是前一个数跟后一个数相比较, 而是在每一次循环内都由一个数去跟 所有的数都比较一次,每次比较都选取相对较小的那个数来进行下一次的比较,并不断更新较小数的下标 这样在一次循环结束时就能得到最小数的下标,再通过一次交换将最小的数放在最前面,通过n-1次循环之后完成排序。 这样相对于冒泡排序来说,比较的次数并没有改变,但是数据交换的次数大大减少。
图解:
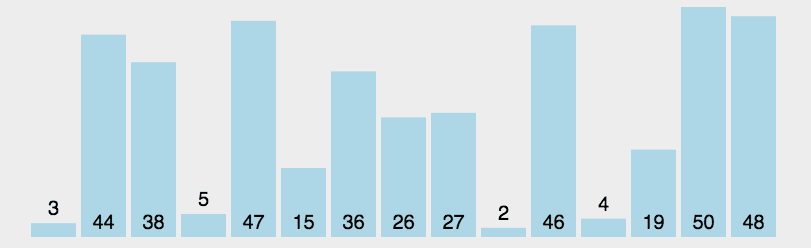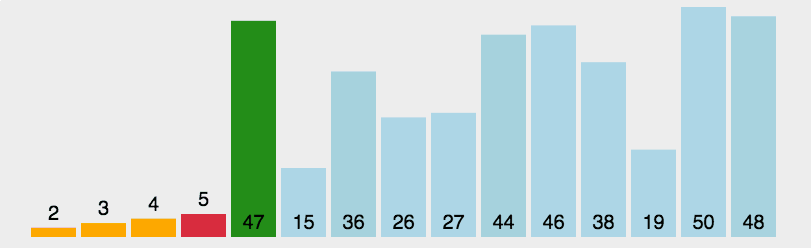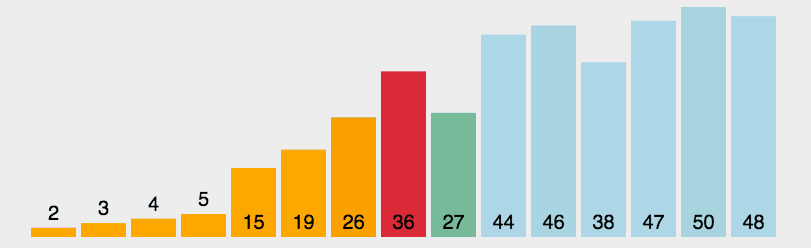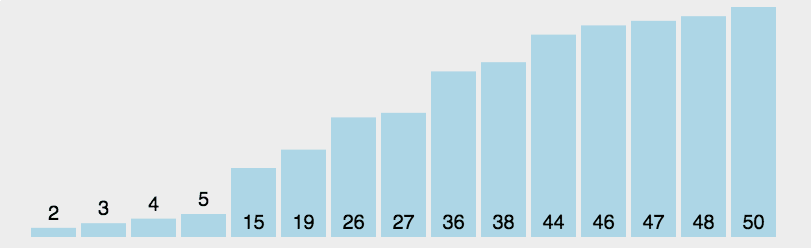
代码实现
public static void sort(int[] arr) {
if (null == arr || arr.length < 2) {
return;
}
for (int i = 0; i < arr.length; i++) {
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) {
minIndex = arr[minIndex] < arr[j] ? minIndex : j;
}
if (i != minIndex) {
swap(arr, i, minIndex);
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
冒泡排序
思想:冒泡排序可以说是最简单的排序之一了,也是大部分人最容易想到的排序。即对n个数进行排序,每次都是由前一个数跟后一个数比较,每循环一轮, 就可以将最大的数移到数组的最后, 总共循环n-1轮,完成对数组排序。
图解:
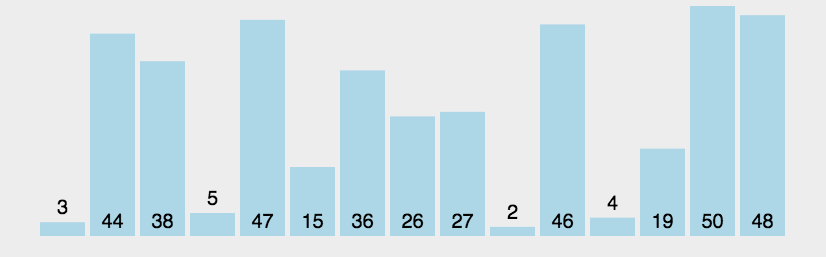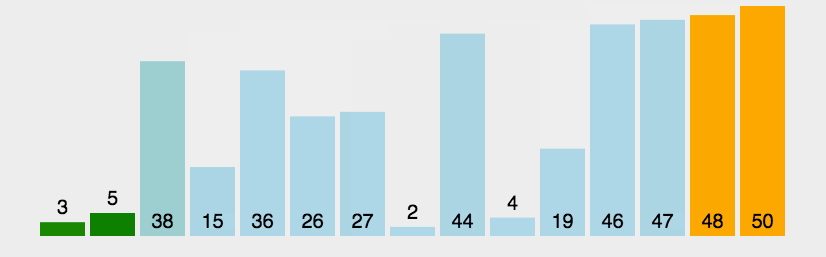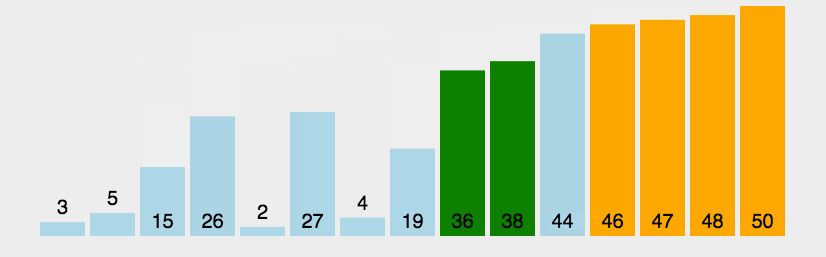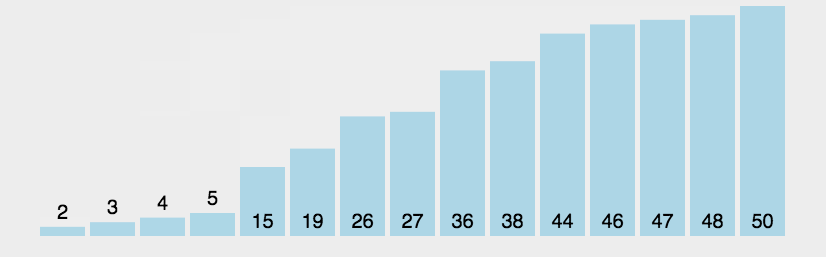
代码实现
public static void sort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}
public static void sort2(int[] arr) {
for (int i = arr.length - 1; i > 0; i--) {
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr, j, j + 1);
}
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
插入排序
思想:是将序列的第一个元素当做已经排序好的序列,然后从后面的第二个元素开始,逐个元素进行插入,直到整个序列有序为止。
图解:
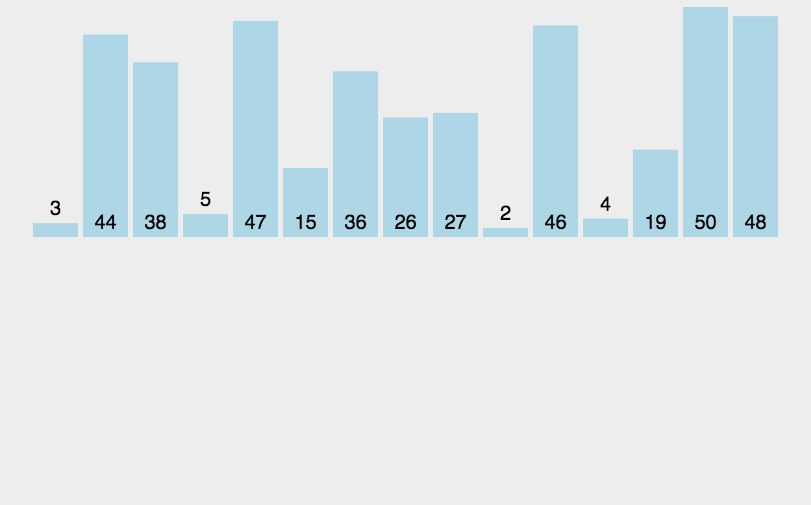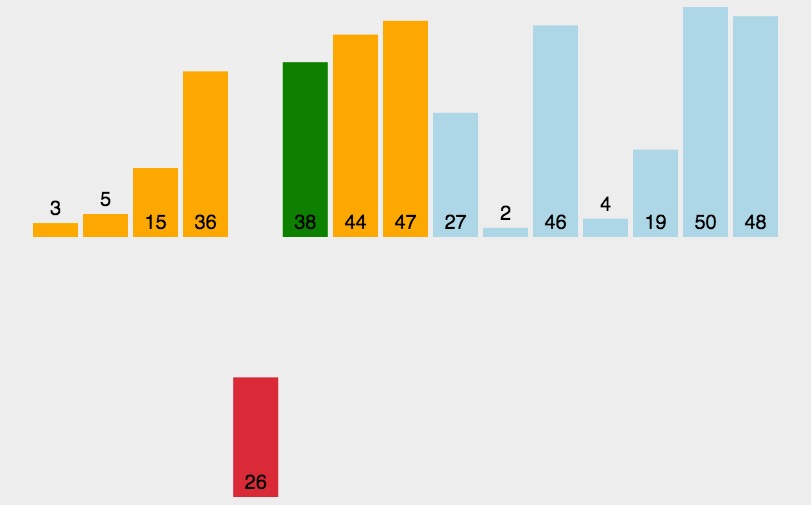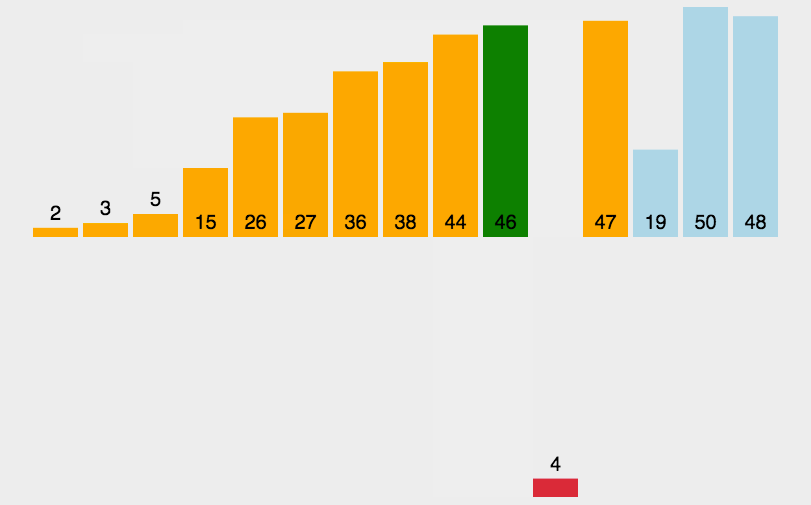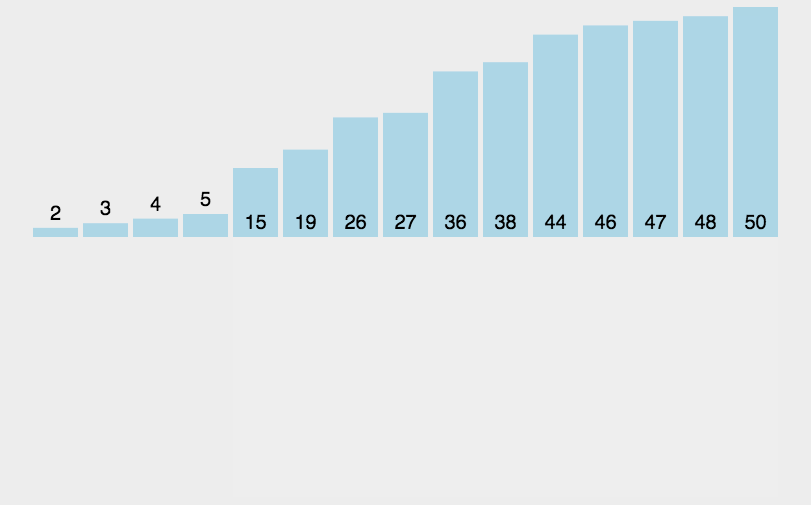
代码实现
public static void sort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
for (int j = i; j > 0 && arr[j] < arr[j - 1]; j--) {
swap(arr, j, j - 1);
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
归并排序
思想:总体概括就是从上到下递归拆分,然后从下到上逐步合并。
递归拆分:先把待排序数组分为左右两个子序列,再分别将左右两个子序列拆分为四个子子序列,以此类推直到最小的子序列元素的个数为两个或者一个为止。
逐步合并:(一定要注意是从下到上层级合并,可以理解为递归的层级返回):将最底层的最左边的一个子序列排序,然后将从左到右第二个子序列进行排序,再将这两个排好序的子序列合并并排序,然后将最底层从左到右第三个子序列进行排序… 合并完成之后记忆完成了对数组的排序操作
图解:
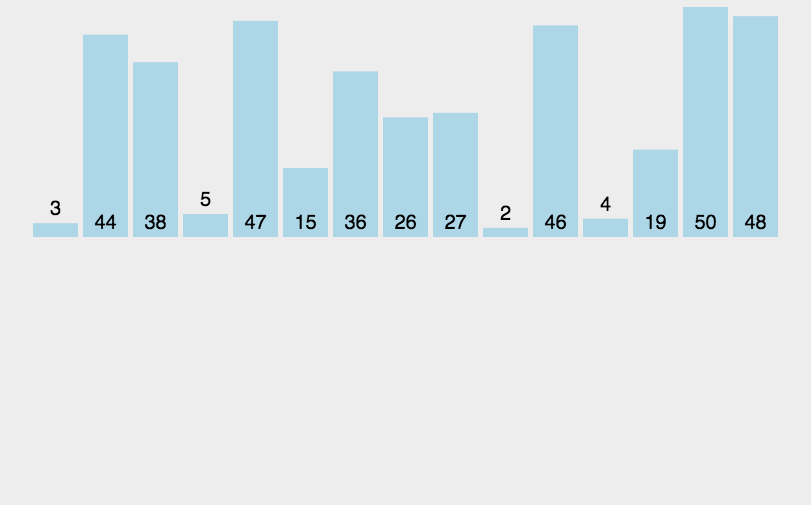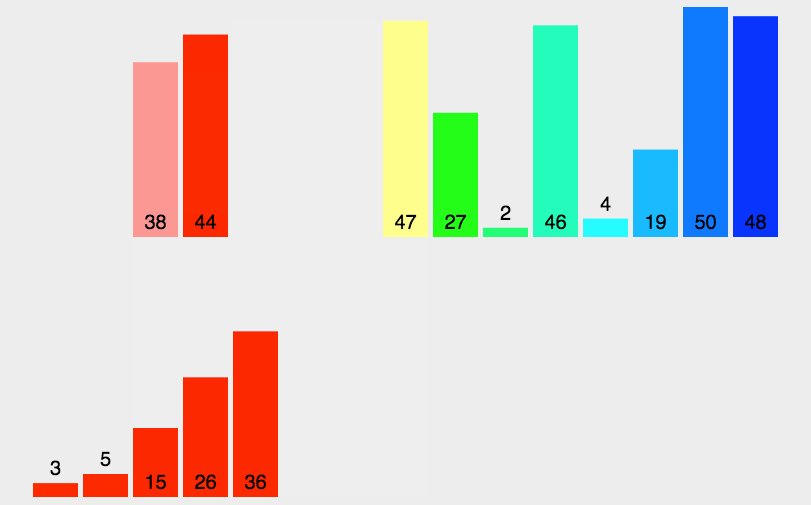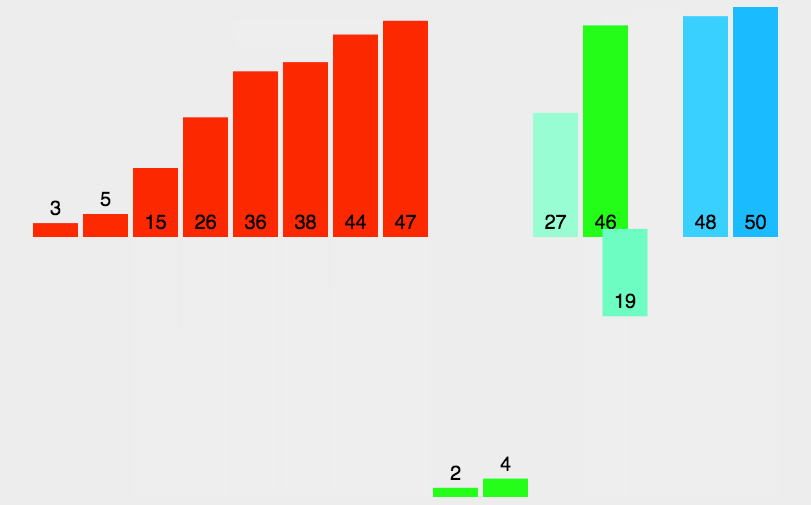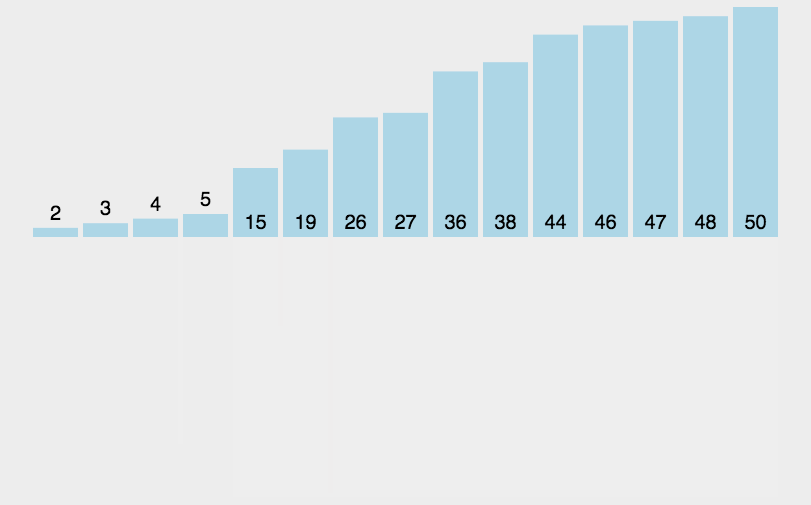
代码实现
public static void sort(int[] arr) {
proceed(arr, 0, arr.length - 1);
}
private static void proceed(int[] arr, int l, int r) {
if (l == r) {
return;
}
int m = l + ((r - l) >> 1);
//左边有序
proceed(arr, l, m);
//右边有序
proceed(arr, m + 1, r);
//左右合并,整体有序
merge(arr, l, m, r);
}
private static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int lb = l;
int rb = m + 1;
while (lb <= m && rb <= r) {
if (arr[lb] <= arr[rb]) {
help[i] = arr[lb];
i++;
lb++;
} else {
help[i] = arr[rb];
i++;
rb++;
}
}
while (lb <= m) {
help[i] = arr[lb];
i++;
lb++;
}
while (rb <= r) {
help[i] = arr[rb];
i++;
rb++;
}
for (int j = 0; j < help.length; j++) {
arr[l + j] = help[j];
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
快速排序(随机)
思想:快速排序也采用了分治的策略,这里引入了‘基准数’的概念。
找一个基准数(一般将待排序的数组的第一个数作为基准数)
对数组进行分区,将小于等于基准数的全部放在左边,大于基准数的全部放在右边。
重复1,2步骤,分别对左右两个子分区进行分区,一直到各分区只有一个数为止。
图解:
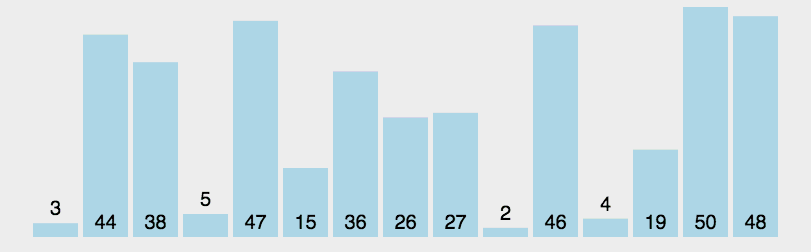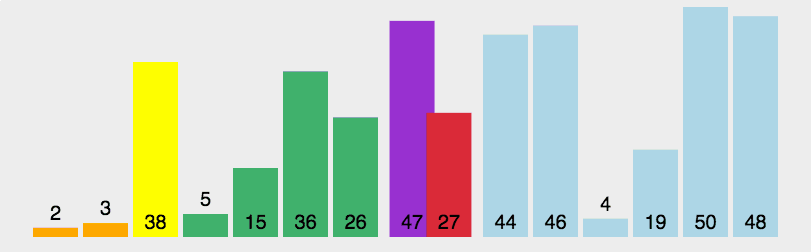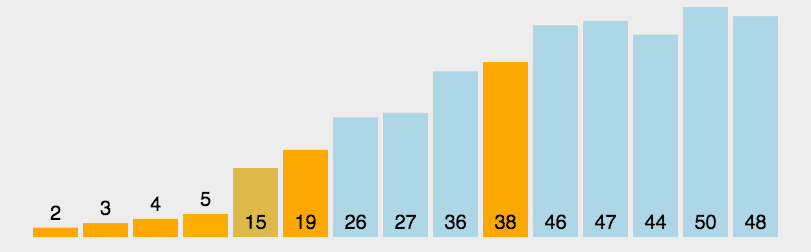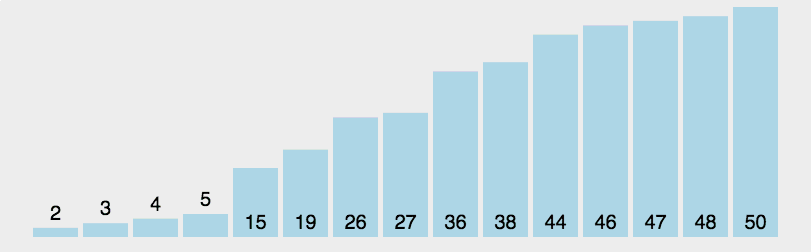
代码实现
public static void sort(int[] arr) {
quicksort(arr, 0, arr.length - 1);
}
private static void quicksort(int[] arr, int l, int r) {
if (l < r) {
int num = l + (int) (Math.random() * (r - l + 1));
swap(arr, num, r);
int[] p = partition(arr,l,r);
quicksort(arr, l, p[0]);
quicksort(arr, p[1], r);
}
}
private static int[] partition(int[] arr,int l,int r) {
int num = arr[r];
int x = l-1;
int y = l;
int z = r+1;
while (y < z) {
if (arr[y] == num) {
y++;
} else if (arr[y] > num) {
swap(arr, y, z-1);
z--;
} else if (arr[y] < num) {
swap(arr, y, x+1);
x++;
y++;
}
}
return new int[]{x, y};
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
}
堆排序
思想:在此之前要先说一下堆的概念,堆是一种特殊的完全二叉树,分为大顶堆和小顶堆。
大顶堆:每个结点的值都大于它的左右子结点的值,升序排序用大顶堆。
小顶堆:每个结点的值都小于它的左右子结点的值,降序排序用小顶堆。
所以,需要先将待排序数组构造成大顶堆的格式,这时候该堆的顶结点就是最大的数,将其与堆的最后一个结点的元素交换。再将剩余的树重新调整成堆,再次首节点与尾结点交换,重复执行直到只剩下最后一个结点完成排序。
图解:

代码实现
public static void sort(int[] arr) {
if (null == arr || arr.length < 2) {
return;
}
//时间复杂度o(NlogN)
for (int i = 0; i < arr.length; i++) {
heapInsert(arr, i);
}
//时间复杂度o(N)
// for (int i = arr.length - 1; i >= 0; i--) {
// heapify(arr, i, 100);
// }
int heapsize = arr.length;
while (heapsize > 0) {
swap(arr, 0, --heapsize);
heapify(arr, 0, heapsize);
}
}
private static void heapify(int[] arr, int index, int heapsize) {
int left = 2 * index + 1;
while (left < heapsize) {
int largest = ((left + 1) < heapsize) && (arr[(left + 1)] > arr[left]) ? left + 1 : left;
largest = arr[largest] > arr[index] ? largest : index;
if (largest == index) {
break;
}
swap(arr, largest, index);
index = largest;
left = 2 * index + 1;
}
}
private static void heapInsert(int[] arr, int i) {
while (arr[i] > arr[(i - 1) / 2]) {
swap(arr, i, (i - 1) / 2);
i = (i - 1) / 2;
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
常见排序算法的时间复杂度,空间复杂度,以及稳定性总结
| 算法名称 |
时间复杂度 |
空间复杂度 |
是否具有稳定性 |
| 选择排序 |
O(N2) |
O(1) |
否 |
| 冒泡排序 |
O(N2) |
O(1) |
是 |
| 插入排序 |
O(N2) |
O(1) |
是 |
| 归并排序 |
O(N*logN) |
O(N) |
是 |
| 快速排序 |
O(N*logN) |
O(logN) |
否 |
| 堆排序 |
O(N*logN) |
O(1) |
否 |
非比较型排序
基数排序
思想:就是将待排序数据拆分成多个关键字进行排序,也就是说,基数排序的实质是多关键字排序。多关键字排序的思路是将待排数据里德排序关键字拆分成多个排序关键字; 第1个排序关键字,第2个排序关键字,第3个排序关键字…然后,根据子关键字对待排序数据进行排序。
图解:

代码实现
public static void sort(int[] arr) {
if (null == arr || arr.length < 2) {
return;
}
int digit = maxbits(arr);
bucketSort(arr, 0, arr.length - 1, digit);
}
private static void bucketSort(int[] arr, int l, int r, int digit) {
int[] help = new int[r - l + 1];
for (int i = 0; i < digit; i++) {
int[] count = new int[10];
for (int j = l; j <= r; j++) {
int k = getDigit(arr[j], i);
count[k]++;
}
for (int j = 1; j < count.length; j++) {
count[j] += count[j - 1];
}
for (int j = r; j >= l; j--) {
int k = getDigit(arr[j], i);
help[count[k]-1] = arr[j];
count[k]--;
}
copyArray(arr, help, l);
}
}
private static int maxbits(int[] arr) {
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
max = arr[i] > max ? arr[i] : max;
}
int digit = 0;
while (max > 0) {
max /= 10;
digit++;
}
return digit;
}
private static void copyArray(int[] arr, int[] help, int l) {
for (int i = 0; i < help.length; i++) {
arr[l] = help[i];
l++;
}
}
private static int getDigit(int num, int i) {
int pow = (int) Math.pow(10, i);
return ((num / pow) % 10);
}

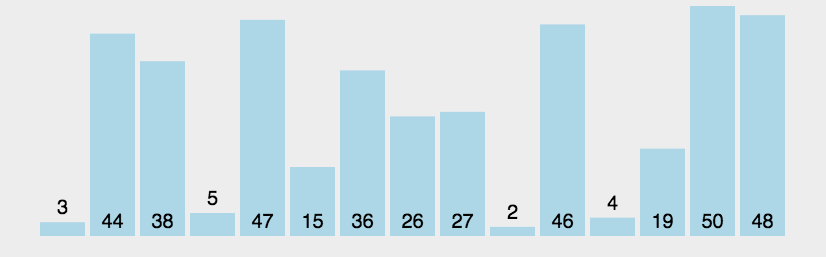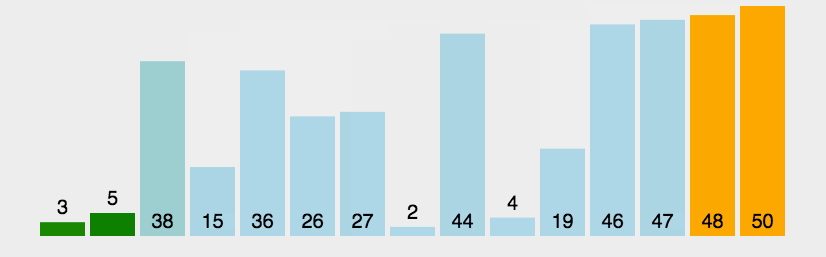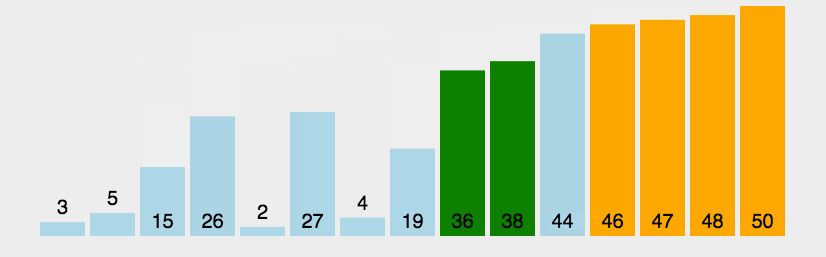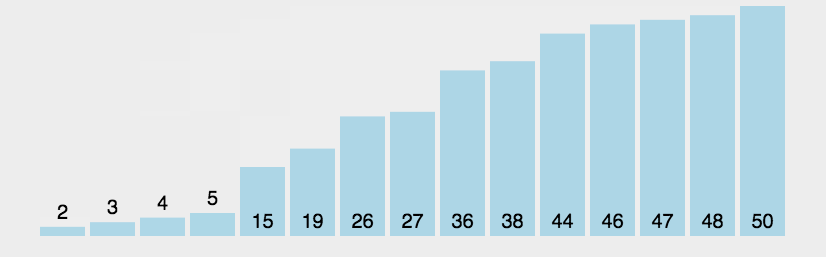








评论区